Ruski matematik rešil 40 let staro matematično zagato

Raziskava je bila objavljena v časopisu Geometric and Functional Analysis. »Problem Lászla Fejesa Tótha je več kot 40 let privlačil matematike, ki se ukvarjajo z diskretno geometrijo. Ta naloga je imela elegantno rešitev, ki smo jo uspeli najti. Ta nas je potem napeljala na misel o drugi, kompleksnejši hipotezi o prekrivanju kroga s premičnimi conami, ki jih dobimo s presekom krogle s tridimenzionalnimi trakovi, ki niso nujno simetrični glede na center,« pravi Aleksander Poljanski, matematik z Moskovskega fizično-tehničnega inštituta.

Ta izrek, kot pravijo znanstveniki, je del t. i. diskretne geometrije - posebne veje matematike, ki preučuje medsebojne odnose geometrijskih likov. Lahko nam odgovori na vprašanje, koliko krogel z enakim volumnom je mogoče postaviti okoli ene takšne krogle. Mnoga podobna vprašanja imajo veliko praktično vrednost, saj so neposredno povezana s problemi na področjih informacijske tehnologije, fizike ali kemije.

Eden od glavnih matematičnih problemov, s katerimi se ukvarjajo predstavniki diskretne geometrije, je t. i. »izrek o trakovih«, ki je bil zastavljen že na začetku 20. stoletja. V svoji osnovi ta matematični problem pravi, da kroga poljubne velikosti ni mogoče prekriti s trakovi, katerih skupna širina je manjša od premera same krožnice. Po pisanju Poljanskega in njegovega kitajskega kolega sta enostavne različice tega problema rešila Alfred Tarski in Thøger Bang že pred 50 leti.

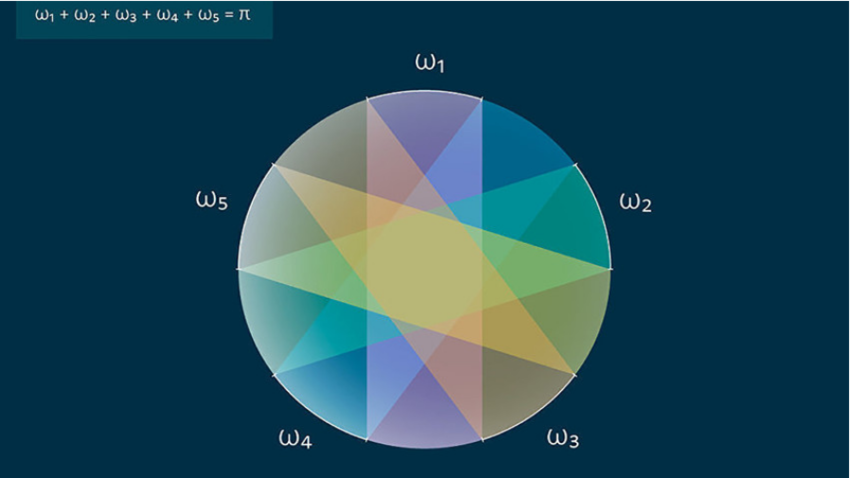
Kompleksno različico omenjenega izreka je leta 1973 razložil madžarski matematik László Fejes Tóth, ki je predpostavljal, da je krožno površino poljubne ploščine mogoče prekriti s poljubnim naborom tridimenzionalnih »plošč« ali trakov, katerih debelina ni večja od dolžine obsega.

Avtorji članka, ki so se naslanjali na idejo Thøgerja Banga, ki je bila uporabljena pri dokazovanju prve večdimenzionalne različice »izreka o trakovih«, so uspeli rešiti ne samo problem Fejesa Tótha, ampak dokazati, da izrek drži tudi v večdimenzionalnem prostoru.

Ruski in izraelski matematik, so enako kot Bang pri dokazovanju šli v nasprotno smer in predpostavili, da bo skupna širina trakov, ki popolnoma prekrivajo krog, manjša od dolžine krožnice.

Raziskovalci verjamejo, da bo njihov dokaz pospešil razvoj diskretne geometrije in omogočil vzpostavitev niza novih matematičnih in praktičnih nalog v zvezi s »izrekom o trakovih«.

Če bi radi uporabili vsebino s spletne strani Russia Beyond (delno ali v celoti), pri svoji objavi dodajte zraven še povezavo na prispevek na naši strani.